Calculando Novas Médias: Uma Abordagem Prática: Como Calcular Uma Nova Média A Partir De Outra Exemplos
Como Calcular Uma Nova Média A Partir De Outra Exemplos – A média aritmética, a mais conhecida das médias, representa o valor central de um conjunto de dados. Sua importância reside na capacidade de resumir informações complexas em um único número, facilitando a compreensão e a comparação de conjuntos de dados. No entanto, situações reais demandam o cálculo de novas médias a partir de dados já existentes, seja pela adição de novos valores, remoção de dados antigos, ou pela alteração de pesos.
Compreender esses métodos é fundamental para análises precisas e tomadas de decisão informadas em diversos contextos, desde finanças até avaliações acadêmicas.
O Conceito de Média Aritmética e Sua Relevância

A média aritmética é calculada somando-se todos os valores de um conjunto de dados e dividindo-se o resultado pelo número total de valores. Sua relevância está na sua simplicidade e capacidade de fornecer uma representação central dos dados. Porém, a média aritmética pode ser influenciada por valores extremos (outliers), distorcendo a representação da tendência central. A necessidade de calcular novas médias surge quando novos dados são incorporados ou quando dados existentes são removidos ou modificados, exigindo um recálculo para refletir a nova realidade dos dados.
Cenários como atualizações de relatórios financeiros, inclusão de novas notas em avaliações escolares, ou a incorporação de novos dados em pesquisas científicas, ilustram a importância da atualização constante da média.
Métodos para Calcular Novas Médias
Calcular novas médias a partir de dados existentes envolve diferentes abordagens dependendo da operação realizada. A adição de novos dados requer a incorporação desses valores no cálculo da média, enquanto a remoção de dados exige a exclusão desses valores antes do novo cálculo. O método para calcular uma nova média após a adição de um novo valor é direto: some o novo valor à soma dos valores existentes e divida o resultado pelo novo número total de valores.
A remoção de um valor segue o processo inverso: subtraia o valor a ser removido da soma total e divida pelo novo número total de valores. A adição de múltiplos valores requer a soma de todos os novos valores à soma anterior, dividindo o resultado pelo número total de valores (antigos e novos).
Exemplo de Cálculo de Nova Média com Adição de Dados

Imagine um conjunto de dados com as seguintes notas: 7, 8, 9, 10. A média é (7+8+9+10)/4 = 8,5. Ao adicionar uma nova nota, 6, a nova média será (7+8+9+10+6)/5 = 8. Observe como a adição de um valor menor diminuiu a média.
| Nota Inicial | Soma Acumulada | Número de Notas | Média |
|---|---|---|---|
| 7 | 7 | 1 | 7 |
| 8 | 15 | 2 | 7.5 |
| 9 | 24 | 3 | 8 |
| 10 | 34 | 4 | 8.5 |
| 6 | 40 | 5 | 8 |
Média Ponderada e suas Aplicações
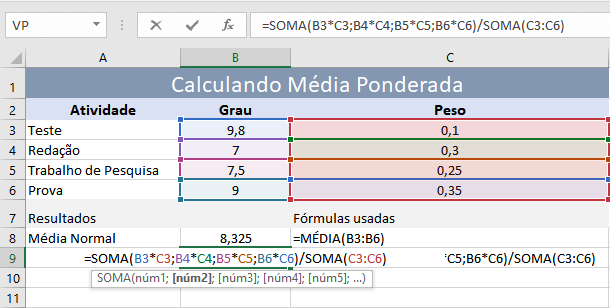
A média ponderada atribui pesos diferentes a cada valor, refletindo sua importância relativa. Em avaliações escolares, por exemplo, provas podem ter pesos maiores que trabalhos. Para calcular uma nova média ponderada após adicionar ou remover pesos, é necessário recalcular a soma ponderada, considerando os novos pesos, e dividir pelo total dos pesos.
Exemplo de Média Ponderada em Avaliação Escolar
Imagine um aluno com as seguintes notas e pesos:
- Prova 1: 8 (peso 40%)
- Prova 2: 7 (peso 40%)
- Trabalho: 9 (peso 20%)
A média ponderada inicial é: (8*0.4) + (7*0.4) + (9*0.2) = 7.
8. Se uma nova prova com nota 9 e peso 20% for adicionada, a nova média será: (8*0.33) + (7*0.33) + (9*0.17) + (9*0.17) = 7.97
Média Móvel e seus Usos, Como Calcular Uma Nova Média A Partir De Outra Exemplos
A média móvel é usada para suavizar flutuações em séries temporais, como preços de ações. Uma nova média móvel é calculada incluindo o novo dado e excluindo o dado mais antigo do período considerado.
Considerações e Limitações do Cálculo de Novas Médias
Erros de cálculo, valores incorretos e outliers podem afetar a precisão da média. Outliers, valores extremamente altos ou baixos, distorcem a média, desviando-a da tendência central real dos dados. Para garantir a precisão, é crucial verificar a consistência dos dados, identificar e tratar outliers, utilizando métodos como a mediana ou a média aparada, em vez da média aritmética simples, quando apropriado.
Uma nova média pode ser enganosa se não levar em conta as mudanças na distribuição dos dados ou a presença de outliers significativos.
Exemplos em Diferentes Contextos
Em finanças, a média de retornos de investimento é crucial para avaliar o desempenho. Em estatística, a média é usada em testes de hipóteses. Nas ciências, a média é usada para analisar dados experimentais. Um cenário onde o cálculo de uma nova média é crucial para a tomada de decisão é a análise de indicadores econômicos, como o PIB, para prever tendências futuras.
Dominar o cálculo de novas médias a partir de dados existentes é uma competência valiosa, aplicável em inúmeras áreas. De simples ajustes em planilhas a análises estatísticas mais complexas, a compreensão dos métodos apresentados aqui permite uma interpretação mais precisa e abrangente dos dados. Lembre-se que a atenção aos detalhes, a identificação de possíveis outliers e a escolha do método apropriado são fundamentais para evitar conclusões errôneas.
Com prática e atenção, você estará apto a utilizar essa ferramenta poderosa para tomar decisões mais informadas e embasadas em dados atualizados e confiáveis. Afinal, a capacidade de interpretar e atualizar médias é um diferencial no mundo cada vez mais quantitativo em que vivemos.

